 Back to the
science index.
Back to the
science index.
 Back to Clive's
home page.
Back to Clive's
home page.Did you know that adding a road to a road network can actually slow traffic? We've all had our suspicions that new roads don't always help, but it can actually be shown mathematically.
Let's start with a simple model of a road network. Our roads will proceed from one junction to another - from A to B - with no side turns; if we want a side turn, we'll make it another junction and so split the road into two. All the roads will have the same speed limit, which for convenience we'll make 60mph (one mile per minute), and all drivers will drive at the speed limit if they can. Finally, let us assume that every road has a single design capacity, in cars per hour. This capacity may be determined by the general design of the road or it may be because of a single pinch-point, but this doesn't matter.
Now we can consider how traffic will behave on a road. Let the road have a length of L miles and a capacity of C cars per hour.
If the actual traffic flow (F cars per hour) is less than the capacity, traffic will flow freely and it will take about L minutes to traverse the road. Of course, as the road gets busier there will be some interference between traffic, and it might take a little longer.
If the actual traffic flow is greater than the capacity of the road, traffic is going to be braking to keep a reasonable distance apart, and there will be people switching lanes to try to overtake slower vehicles. As the road gets busier, you start to get stop-start behaviour in places. A reasonable model is that the time taken to traverse the road is proportional to the amount of traffic as well as to the length.
Combining these two, we can come up with a formula: the time taken to traverse a road (T minutes) is:
(yes, there is a minor glitch when C = F, but let us ignore this).
Let's consider the following road network:
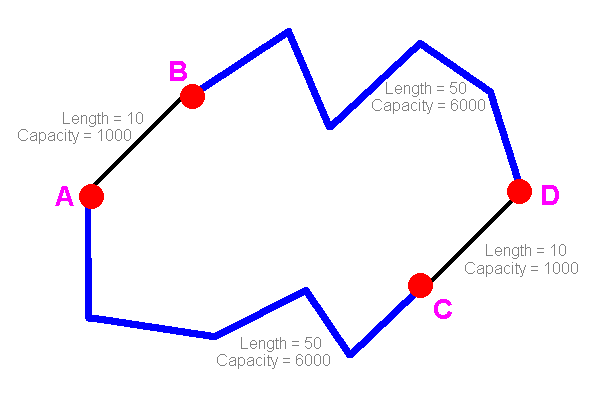
There is a lot of traffic flowing from A to D; say 6000 cars per hour. There are two routes, one via B and the other via C (both of which are tiny villages that don't generate any noticeable traffic themselves). Each route consists of a long high-capacity section and a short low-capacity one. The length of time to get from A to D via a route will depend on the amount of traffic on that route, and thus on the split between the routes:
| Cars per hour travelling | Time taken from A to D | ||
|---|---|---|---|
| via B | via C | via B | via C |
| 0 | 6000 | 60 | 116 |
| 1000 | 5000 | 62 | 105 |
| 2000 | 4000 | 72 | 94 |
| 3000 | 3000 | 83 | 83 |
| 4000 | 2000 | 94 | 72 |
| 5000 | 1000 | 105 | 62 |
| 6000 | 0 | 116 | 60 |
We can see that if traffic is split unevenly, one route will be faster than the other. People using the slower route will realize that they could do better by changing to the other, and no doubt will do so. The only stable situation is where half the traffic goes each way, because then anyone changing to the other route will find they are on a slower route, and thus will change back. Therefore the stable situation for this network is when the journey takes 83 minutes.
Now suppose that the local council notices that B and C are actually quite close, and there's no real reason for all the traffic to go along one of these two long roads. So they build a brand-new link from B to C with plenty of capacity. However, since it involves a different budget, they don't improve the existing roads.
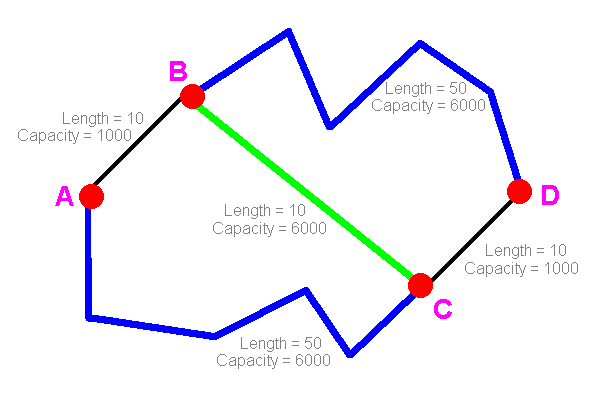
Now there are three sensible routes from A to D, and the time taken on each will depend on the traffic on all of them. For example, suppose we assume that people will behave symmetrically, so that the same number of people use each long road. Then we get:
| Cars per hour travelling | Time taken from A to D | |||
|---|---|---|---|---|
| via B | via both | via C | via B or C | via both |
| 0 | 6000 | 0 | 110 | 136 |
| 500 | 5000 | 500 | 105½ | 125 |
| 1000 | 4000 | 1000 | 101 | 114 |
| 1500 | 3000 | 1500 | 96½ | 103 |
| 2000 | 2000 | 2000 | 92 | 92 |
| 2500 | 1000 | 2500 | 87½ | 81 |
| 3000 | 0 | 3000 | 83 | 70 |
From this we can see that people will start using the new link because it is somewhat faster. However, by doing so they will increase the traffic on both the overloaded sections of road, increasing travel time for everyone. The situation will be stable when all three routes carry the same traffic: if people shift to the other route, they will find that they are on the slower of the two routes and will switch back. So the only stable position is when everyone takes 92 minutes for the journey.
But this is 9 minutes (almost 11%) slower than before the new road was opened!
Note that if people would avoid the new route, their journey would speed up. But if people "cheat" they will do better, and soon the flows come back to the stable position.
The only way to speed up traffic is to close one of the roads! This is the Road Network Paradox.
If all this seems a bit esoteric, there is a simple physical equivalent. Consider the following network of springs and strings:
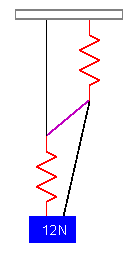
If all the strings are taut, then each of them will be carrying one-third of the weight of the block. So if the purple string is cut, the remaining strings will carry more of the weight and the block will drop down a bit as the springs take up the load, right?
Wrong!
As shown, each string has a tension of 4N, so the springs will each be under a tension of 8N and will stretch accordingly. Now, when the purple string is cut the remaining strings have a tension of 6N, and so does each spring. So there is less tension in the springs, and they will contract accordingly, making the block rise.
This simple physical example is the exact analogy of the road network we've discussed.