Link analysis has been seen for many years as a useful tool for law enforcement. However, it is at the moment primarily used as an analytical tool after the fact of a crime.[1] On the other hand, studies of legitimate networks tend to focus on efficient design or resilience following a problem[2]. The resulting lack of cross-connection between these topics means that law enforcement lacks techniques for the active use of the graphical descriptions of criminal networks that link analysis provides, such as by indicating the best way to attack and disrupt them.
For example, [Kre] examines the network formed by the 19 hijackers of September 11th 2001 and their 43 known associates. If the authorities had had this network diagram available to them beforehand, how many and which members should they have concentrated their efforts on catching? How effective would it have been to remove two or three individuals from the network?
This essay attempts to address some of these issues by examining a legitimate trust network and determining by a set of experiments how much effort is required to disrupt it. I then apply the same techniques to covert networks and attempt to draw conclusions for law enforcement. The legitimate trust network in question is the PGP "web of trust", which is perhaps the commonest instantiation of public-key encryption and digital signatures. Since these may be unfamiliar to my readers, I start by describing them before explaining my own research into this network and ways to attack both it and other networks.
Encryption is a technique for keeping communications secret that has existed for thousands of years.[3] If Alice wishes to send a message to Bob but wishes to ensure that Eve[4] can't read it if she intercepts it, Alice will encrypt the message and Bob will have to decrypt it. Traditional or "symmetric" encryption involves a secret that Alice and Bob know but Eve does not. Alice uses this secret - the "key" - and an algorithm to encrypt the message. Bob uses the same key and a related algorithm to decrypt the message again. Assuming that the encryption method is strong enough and Alice and Bob keep the key secret, Eve will not be able to decrypt the message. (While in principle the algorithm can be a part of the secret, in practice it needs to be public and secrecy should reside only in the key, a rule first stated in [Ker]. In general, detailed public scrutiny by experts is needed to identify weaknesses in an algorithm.)
Symmetric encryption actually provides two facilities. Firstly and obviously, it allows a message to be sent securely across an insecure route. But secondly, and more subtly, it allows Bob to verify that the message is authentic; that is, it actually came from Alice and not an impostor, since only Alice knows the key. Note that Bob cannot convince a third party of this fact, however, since he could have forged the message as he also knows the key. A classic example of how users of a cypher rely on the authenticity property can be found in [Doy].
Until the mid-1970s, all known cryptographic systems required the use of a secret key shared between the correspondents, which therefore required them to meet or to use a trusted courier, and management of these keys was often seen as the biggest problem with cryptography. However, in 1976 a seminal paper by Diffie and Hellman [Dif] showed how Alice and Bob could create a shared secret using only communications over an insecure path - that is, even though Eve could read every message Alice and Bob sent to each other, they could still create a key that both knew but Eve did not. This was followed in 1978 by [RSA] which used a related technique to create an encryption system that did not involve shared secrets but instead used a published - or "public" - key.
In public-key, or asymmetric, encryption, Bob creates two separate keys, known as his public key and his secret key. While these are related, they have two important properties: a message encrypted using one key can only be decrypted using the other, and not the original key, and it is not possible for a third party such as Eve to deduce the secret key when she only knows the public key. Therefore Bob can now publish his public key to the entire world. Alice can encrypt the message using Bob's public key and know that only Bob can decrypt it, because only Bob knows his secret key. Though, as we shall see, this does not eliminate the key distribution problem, it certainly simplifies it because public keys don't need to be kept secret and secret keys don't need to be sent to another person.
However, it should be noted that the authentication property of symmetric encryption has been lost: when Bob receives a message, he cannot tell who actually wrote it since the whole world knows his public key. Luckily public-key encryption has a solution to this. Suppose that Alice also generates a public key and a secret key and publishes the former. Before encrypting the message to Bob using his public key, she first encrypts it using her own secret key[5]. When Bob receives the message, he must decrypt it twice: first using his own secret key, and then using Alice's public key. The outer encryption ensures that nobody else can have read the message, but the inner one proves that Alice must have sent the message since she is the only person who knows her secret key. Furthermore, Bob can demonstrate this to a third person, since he cannot have created the message either.
Since this authentication process shares many of the properties of written signatures, it is known as a digital signature, and the process of encrypting a message so that anybody can decrypt it is called signing the message.
PGP (Pretty Good Privacy) is an implementation of public-key encryption. It was first released by Phil Zimmerman in 1991 as a free package to provide public-key encryption and signatures for messages sent by e-mail. Since then it has been commercialised and other features have been added, but it continues to provide these original facilities.
The most important feature about PGP was and remains that it provides a simple and extensible format for representing public keys, secret keys, encrypted messages, signed messages, and the other paraphernalia involved in using public-key encryption. In particular, it allowed for key signing. The data formats and algorithms used in PGP are completely public (the former can be found in [Cal]) and compatible software packages exist, of which the best known is GPG (Gnu Privacy Guard), which is available free.
A problem with the Alice and Bob scenario described above has been glossed over: how does Alice know that she has a genuine copy of Bob's public key, and not Eve's key labelled as Bob's? One way is for her to obtain it directly from Bob, or via a trusted channel, but this is not always possible. One of the major strengths of PGP is that it addresses this problem through the concepts of key signing and trust chains.
Key signing is the process of using one key to digitally sign another. Suppose that Alice and Bob have a mutual friend Fred. Alice possesses a copy of Fred's public key but not Bob's. Fred visits Bob and signs a copy of his public key, giving the signed copy back to Bob. Bob can now send Alice the signed copy, or can publish it anywhere that Alice can read it. She can verify Fred's signature using his public key and, having done so, and provided she trusts Fred to have checked that his copy of Bob's public key is genuine, she now knows she has a genuine copy of Bob's public key.
This process does not have to end with one intermediary. Perhaps Fred doesn't know Bob, but the two of them have a mutual friend in Michaela. Alice needs to obtain three pieces of data: a copy of Bob's key signed by Michaela, a copy of Michaela's key signed by Fred, and a genuine copy of Fred's key. She uses Fred's key to verify Michaela's, and then Michaela's to verify Bob's. Obviously she needs to trust both Fred and Michaela in this process, but this "chain of trust" allows her to obtain a genuine key from someone who she has never met without a go-between.
Because there is nothing secret about these signed keys, they can be and are published on specialised servers. By treating keys as nodes in a graph and the operation "key P was signed using key Q" as a (directed) arc, the set of published keys forms a graph or web[6] which Alice can use to find a path to verify a key. Using a signed key involves trusting the signer, and therefore this graph has become known as the web of trust.
Most social networks involve a concept of trust. For all but the smallest networks, it is impossible for everybody to know everybody else and to only communicate in person. Therefore members have to rely on each other to verify the identity and reliability of other members. In essence, Alice is willing to deal with Bob because Fred vouches for Bob and Alice trusts Fred's judgement. If it were possible to chart these trust relationships, we would end up with a graph not dissimilar to the PGP web of trust.
Guardiola et al. seem to have been the first to recognise, in [Gua], that the structure of the PGP web of trust may tell us something about trust networks in general. Using data from July 2001, they found that the web comprised 191,548 individuals with 286,290 directed links between them. The connections were not random but, rather, consisted of "a macro scale-free structure with micro strongly-connected cells in a complex network", with a number of highly-connected "super-nodes" linking the cells. They reported that a deliberate attack on the network could easily separate the cells from one another but could not disrupt their internals.
I attempted to repeat and extend their work using the web of trust as of December 2007. It is no longer possible simply to download the entire web, nor to do bulk searches with more than about 500 responses. Instead it is necessary to query servers for each key individually; the server then returns a list of keys that have signed that key. Therefore I started with an initial set of about 8,000 keys found in various ways (e.g. all those with "Clive" or "Katy" in the associated email address) and then downloaded them, found the keys that had signed them, downloaded those, and so on until no new keys were found. This resulted in a total of 83,138 separate keys. Of these, 77,401 were on the key servers used while the other 5,737 were not but only appeared as signatures. There were a total of 481,383 signatures.[7]
Table 1 shows the number of nodes with a given number of signatures (the in-degree of the node) or which sign a given number of others (the out-degree). The highest in-degree was 1,274[8] and the highest out-degree 6,799[9], while the means were 6.22 (in-degree) and 5.79 (out-degree).
| N (degree of node) |
Number of nodes signing N others (out-degree) |
Number of nodes signed by N others (in-degree) |
| 0 | 5995 | 14281 |
| 1 | 33408 | 18849 |
| 2 | 13287 | 11589 |
| 3 | 7306 | 7465 |
| 4 | 4541 | 4881 |
| 5 | 3160 | 3591 |
| 6 | 2126 | 2411 |
| 7 | 1669 | 1834 |
| 8 | 1315 | 1429 |
| 9 | 1063 | 1090 |
| 10 to 19 | 4794 | 5266 |
| 20 to 29 | 1630 | 1655 |
| 30 to 99 | 2318 | 2543 |
| 100 to 999 | 523 | 514 |
| 1000 to 1600 | 2 | 3 |
| 6799 | 1 | |
| Total | 83138 | 77401 |
Table 1 | ||
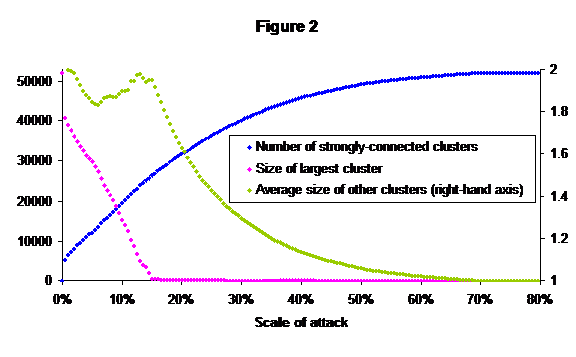
Figure 1 shows the same data as a log-log plot; as can be seen, it approximately fits a power law with exponent -1.9 (compare with the -1.7 and better fit found by Guardiola et al.).
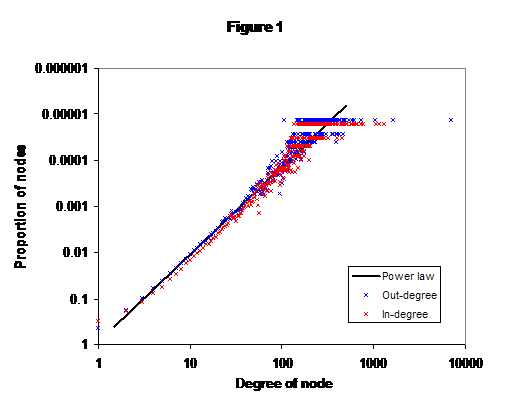
Using the algorithm of [Tar] to divide the keys into strongly-connected clusters (that is, sets of keys where there is a path from any key in the cluster to any other), the dataset contained:
The remaining analysis was carried out on the large cluster, which involved 429,848 signatures in total, dividing into 172,118 one-way and 128,865 mutual signings.
The attack suggested in [Alb] involves systematically removing a proportion of the nodes (the "scale" of the attack) starting with the most-connected. As can be seen in figure 2, almost immediately the size of the largest cluster starts dropping until, by about 15%, the network is essentially disconnected (though it is only at 80% that it is completely so); even attacking a single node removes nearly 11% of the nodes from the cluster. The green line in the figure shows the average size of all strongly-connected clusters other than the largest; as can be seen, the average is never significantly greater than 2, indicating that the majority of these clusters are actually isolated nodes. These results agree with those in [Gua].

However, I suggest that the average size of the other clusters is not the best measure of the disconnectedness of the network. For this paper I define a mid-size cluster as being any cluster other than the largest that includes at least 3 nodes, so that it is possible to attack it other than by breaking it into singletons; the largest mid-size cluster is, of course, the second-largest cluster in the network. Figure 3a shows the largest mid-size cluster, the largest cluster (once that falls below 500), and the ratio of largest to second-largest.
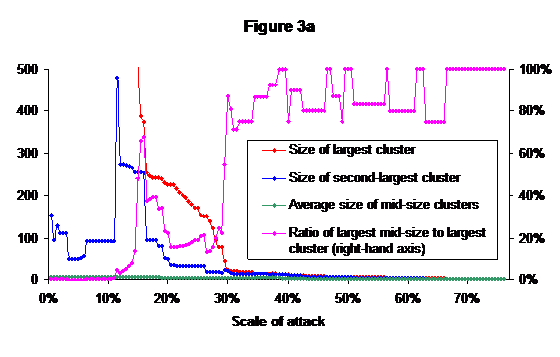
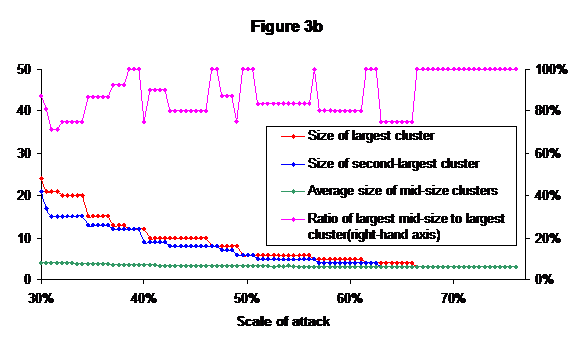
It can be seen that the second-largest cluster remains far smaller than the largest until the network is falling apart completely at about the 15% attack level. The average size of mid-size cluster remains tiny, never reaching as high as 8. Figure 3b shows the same data on a larger scale for levels of attack of 30% or above.
What this analysis shows is something rather different from the results of [Gua]. Rather than collection of small clusters held together by a larger-scale structure, there is a single large cluster that flakes off smaller ones as it is attacked. Indeed, figure 2 shows an almost linear decrease in size with the scale of the attack. Furthermore, the individual pieces also fall apart under the attack - note how the second-largest cluster halves in size around the 3% attack level. Whilst the model of [Gua] is like a comet: a collection of small strong rocks held together by a weaker superstructure that melts away easily, my results offer a model more like an ice-shelf melting in the spring and throwing off hundreds of small icebergs from its edge as it does so.
If PGP provides a valid model of social networks, these results should be applicable to real-world networks. One such is the network of the September 11th hijackers and their associates. The diagram in [Kre] shows a total of 62 people and 153 links. Using the same attack methodology we get the results in figure 4.
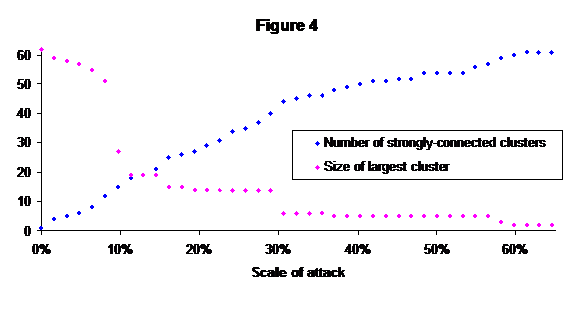
Once again we see that the network is largely disrupted by about the 15% level of attack, though it takes much more (41 of the 62 nodes) to completely disconnect it. The pattern is not identical to that of the much larger PGP network, but it is not dissimilar either.
The "traditional" covert network is designed on a "cell" basis to minimize the number of members that can be compromised by a traitor. In its purest form, it consists of a number of layers of cells: each cell consists of three people plus a cell leader from the layer above, with each member being the leader of their own cell in the layer below:
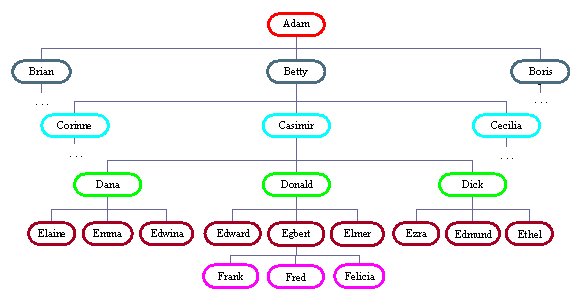
A brief discussion in chapter 5 of [Hei] points out that networks of this form fall apart as soon as a single internal node is removed and suggests two methods of curing this: either providing a way to send messages up through the structure (e.g. from Fred to Donald or Casimir), or to send them sideways to other sub-trees (e.g. from Elmer to Ezra). In fact, removing one interior node at random from such a network with N levels will isolate, on average, 3N-4.5 nodes[10]. I therefore tried each of these three strategies in turn, removing interior nodes at random until the remaining nodes stopped forming a strongly-connected cluster. With 6000 trials in each case on a 6-layer network (121 interior and 364 total nodes), I found the number of nodes needing to be removed was:
| Strategy: | link up 2 levels | link up 3 levels | link sideways |
|---|---|---|---|
| minimum | 2 | 2 | 3 |
| maximum | 28 | 49 | 110 |
| mean | 7.5 | 10.9 | 41.8 |
| median | 7 | 9 | 42 |
| mode | 5 | 6 | 43 |
| modal trials | 10.9% | 8.1% | 3.3% |
("modal trials" is the proportion of trials that removed exactly the modal number of nodes).
All three strategies are proof against a single attack but bad luck means that removing only two or three nodes could be sufficient to partition the network. Despite having about 17% less links than the others (each node except the one at the root of the tree has 7 links outwards and 7 inwards), the arrangement with sideways links is clearly superior to the others, requiring on average about one-third of the interior nodes to be removed before it separates into two (though this is only about 11% of the entire network).
An organised network of criminals, whether formal or informal, will be held together by links of trust. Every member of the network needs to be able to have trust in every other member; after all, if any one person betrays the criminal enterprise to the authorities then all of the members of the network are at risk of conviction and imprisonment. This trust can be direct - Fred knows Jim and trusts him - or indirect - Fred doesn't know Sheila, but is willing to accept Jim's recommendation because, after all, Jim has as much to lose if Sheila betrays them (or even more: at least initially, Sheila won't know who Fred is). The mapping to the PGP web of trust is obvious. The more interesting question is whether it provides new insights into such networks.
Traditionally the role of the police has been either to investigate crimes after they have been committed and catch the criminals, or to determine when a crime is going to be committed and arrest the perpetrators "red-handed". However, there are a number of situations where neither of these is the desirable course of action. One obvious example is that of terrorist groups. It is clearly undesirable to let the group carry out their plan before catching them, while stopping them in the act - particularly with suicide attacks - is fraught with danger for both police and public. Equally, while the group is still in the planning stage it can be hard to act overtly against them - even if they are in the same country, there may be no offence to charge them with. This leaves the alternative of disrupting the network, perhaps by deporting members who are not residents, finding a minor charge to hold people on, or simply by making it clear to the group that the authorities are watching them. Similar considerations apply to spy networks.
Another example that is particularly applicable to modern times are networks of paedophiles who exchange images of child abuse. These networks often spread through several countries and it can be difficult or impossible to locate all of the members. They are also often very large compared with other criminal enterprises: one network reported recently in [Eur] allegedly contains 12,000 members in Germany as well as spreading to 70 other countries, while the 1999 "Operation Ore" identified 7,000 suspects in the UK (though it is less than clear how many of these actually purchased child abuse images, and in any case the "network" is a trivial one with a single central node and no known links between any others). With such numbers it can take the police years to identify and investigate all the members, during which time they can carry on their activities. Therefore the best strategy for the authorities to take is to attempt to disrupt these networks and so make it impossible, or at least more difficult, for the exchanges to take place. The illicit "peer to peer" networks used for dissemination of music and films in breach of copyright are also very similar and the same considerations apply.
Disruption of a network can take two forms. One is to block the communications between its members, while the other is to remove or compromise the members themselves (in graph theory terms, the former removes arcs while the latter removes nodes). Blocking communications without knowledge of who is communicating requires being able to identify the communication paths used and to ensure that no alternatives exist. For terrorist and espionage groups, this is clearly impossible - the number of ways that people can communicate covertly is limitless, from leaving chalk marks on walls to carefully phrased announcements on the radio[11]. Even within such restrictive environments as prisons and POW camps, history is replete with examples of covert communication channels. The problem remains similar in the case of paedophile groups. Even if the Internet is the only channel allowed, it is easy to hide messages among the "noise" of everyday traffic. There is no easy way to identify illegal images automatically; indeed, it is arguable that it cannot be done at all. For example, the very definition of illegality[12] includes an arbitrary boundary:
1.(1) It is an offence for a person -
(a) to take, or permit to be taken or to make, any indecent photograph or pseudo-photograph of a child; or
(b) to distribute or show such indecent photographs or pseudo-photographs; or
[...]
7.(6) "Child", subject to subsection (8), means a person under the age of 18.[13]
Thus if identical-looking photographs of the same person are taken on consecutive days, one could be illegal and the other legal. Even when age is not an issue, the definition of "indecent" is somewhat subjective, and it is likely that blurring of a few strategic pixels could make the difference between legality and illegality. Even if such images contained clear and obvious stigmata, there are a range of techniques available for concealing them: the data forming the image can be scrambled, or it can be split into parts so that the identifying characteristics are also split up and thus vanish. Finally, it cannot be assumed that (say) standard e-mail is being used: as well as a range of other standard communications protocols (such as NNTP, FTP, Instant Messaging, etc.), a strength of the Internet is that non-standard protocols can be designed and used. Certainly it is not possible, for example, to say that "illegal material is only transmitted on port 6969" or "messages containing illegal material will always include the string 'paedophile' within them" and block all such traffic.
Having dismissed the practicalities of disrupting the communications between members of the network, we are left with the option of removing some of its members. The way in which this happens is largely irrelevant (for example, in some contexts it is sufficient to let someone know that they have been detected to remove them from the active network); what is significant is which members to remove and what effect this has on the network. We can now apply the lessons of the previous sections and see their implications for law enforcement.
The PGP web of trust is an example of a network that grows by recruitment, with existing members introducing new ones. This is probably a good model for a paedophile network or a criminal gang. On the other hand, the September 11th network is an example of a network constructed for a specific purpose and where links were created to meet specific needs (e.g. for the supply of funds). Both of these types of network have the property that the specific structure of the network was not a consideration when it was built (though [Kre] points out that the September 11th network deliberately reduced the number of links in order to aid secrecy). For these types of network, the analysis shows that it is necessary to remove around 15% of the most-connected nodes before the network starts to break up. Of course, as [Kre] also points out, not all nodes are equal: if you can remove a person with key skills, this will do more damage than would be predicted from connectivity. This is relevant to the September 11th network but not to paedophile ones.
This is bad news for law enforcement. A large paedophile network will be almost impossible to disrupt simply by arresting a few of its members. It will be necessary to identify a large enough number that the network will break into pieces when they are arrested - for the network described above, this means nearly 2,000 people. Furthermore, all must be arrested simultaneously or nearly so, not just so that they cannot warn each other so that any evidence is destroyed, but also to ensure that any self-repair mechanisms in the network cannot nullify the effects of the attack. For example, assume that the members of a paedophile network communicate using specialised software. This can be designed, on a specific command, to broadcast a "this node is being removed" message over the network which automatically causes each of its neighbouring nodes to be told of a replacement contact - removal of a node and its associated links thus causes new links to be created.
Consideration of self-repairing networks leads us to the type of network specifically designed to be resistant to attack, of which the "cell" network is the exemplar. As we saw above, it is possible to design such a network so that even if a large amount of the network (one-third or more) is removed, it remains in one piece even though each node has relatively few links. No doubt a more sophisticated design could be even more resilient for a similar number of links per node. If the previous conclusions were bad news for law enforcement, this is even more so: an intelligent opponent can create a network that cannot easily be disrupted short of completely destroying it.
Analysis of both an existing trust network and a former criminal network shows that it requires removal of about 15% of the most-connected nodes to serious disrupt the structure of the network. Covert networks specifically designed against attack are even harder to disrupt. The implications for law enforcement are that it is impractical to disrupt such networks merely by removing a few participants and expecting the structure to "wither on the vine". Rather, efforts should be directed towards identifying and neutralising as many participants as possible.
[1] In the UK, police forces apparently use a link analysis package called WATSON, mentioned briefly in [Mat]. For more details on link analysis, see [RCM] for an overview of the ViCLAS system used by the Royal Canadian Mounted Police and [Sch] for the use of link analysis by the Tucson Police Department.
[2] For example, network problems often lead to an event called "route flapping"; see [Smi] for discussion of this and how to reduce it.
[3] For a long but eminently readable history of cryptography and cryptanalysis, see [Kah]; a shorter but less comprehensive treatment is available in [Sin]. Both include extensive bibliographies for the interested reader.
[4] Cryptography examples traditionally use Alice, Bob, and Eve. See also [Gor].
[5] For technical reasons a more complicated process is used in practice, but the difference is not germane to this paper. Details can be read in [PGP].
[6] This term came into use before the widespread use of "web" to mean the World Wide Web.
[7] For technical reasons, each key is required to sign itself. These self-signatures are excluded from all counts in this analysis.
[8] This is a revoked key of Phil Zimmermann.
[9] This is an automated service which will sign any key where it can verify the email address associated with that key.
[10] For N = 1 to 5 the actual values are 0, 3, 5.25, 7.85, and 10.65 nodes; beyond this the approximation is accurate to better than 0.5%.
[11] The interested reader is directed to the works of J.le Carré, F.Forsyth, and T.Clancy for further details.
[12] Protection of Children Act 1978.
[13] The copy of the Act in the Statute Law Database still gives an age of 16, but this was altered by s.45 of the Sexual Offences Act 2003.
My tutor, B. Schafer, first pointed me at [Gua] and suggested that I examine how the vulnerabilities of trust networks can be applied to attacking paedophile networks.
All online sources were successfully accessed on 4th January 2008.
[Alb] R. Albert, H. Jeong, and A-L. Barabási, Error and attack tolerance of complex networks, Nature 406, 378-382 (2000).
[Cal] J. Callas, L. Donnerhacke, H. Finney, and R. Thayer, OpenPGP Message Format, IETF RFC 2440, November 1998. Available: http://www.ietf.org/rfc/rfc2440.txt
[Dif] W. Diffie and M.E. Hellman, New directions in cryptography, IEEE Transactions on Information Theory 22 (1976), 644-654.
[Doy] Sir A.C.Doyle, The Adventure of the Dancing Men, The Strand Magazine December 1903 and Collier's Weekly December 5, 1903, and included in the collection The Return of Sherlock Holmes. Available: http://www.thevoiceofreason.com/sherlock/downloadebooks/TheAdventureOfTheDancingMen.pdf
[Eur] Vast German police operation against paedophiles, Euronews 26th Dec 2007. Available: http://www.euronews.net/index.php?page=info&article=461431
[Gor] J. Gordon, The Story of Alice and Bob, after-dinner speech, April 1984. Available: http://www.conceptlabs.co.uk/alicebob.html
[Gua] X. Guardiola, R. Guimeà, A. Arenas, A. Diaz-Guilera, D. Streib, L.A.N. Amaral, Macro- and Micro-structure of Trust Networks, arXiv:cond-mat/0206240v1. Available: http://arxiv.org/abs/cond-mat/0206240
[Hei] Robert A. Heinlein, The Moon is a Harsh Mistress, published 1966 by Putnam in the USA, latest UK publication 2005 by Hodder & Stoughton, ISBN 0340837942.
[Kah] David Kahn, The Codebreakers, published 1967 by MacMillan (no ISBN). New chapter added 1996, ISBN 0684831309.
[Ker] Auguste Kerckhoffs, La cryptographie militaire, Journal des sciences militaires, vol. IX, pp. 5-83, Jan. 1883, pp. 161-191, Feb. 1883. Available: http://www.petitcolas.net/fabien/kerckhoffs/
[Kre] Valdis E. Krebs, Uncloaking Terrorist Networks, First Monday, volume 7, number 4 (April 2002), Available: http://firstmonday.org/issues/issue7_4/krebs/
[Mat] Robert Matthews, Resistance is Futile, New Scientist, issue 2102, 4 October 1997. Available: http://technology.newscientist.com/channel/tech/forensic-science/mg15621029.000
[PGP] Network Associates Inc., How PGP Works, extracted from the PGP 6.5.1 documentation. Available: http://www.pgpi.org/doc/pgpintro/
[RCM] Royal Canadian Mounted Police, Violent Crime Linkage Analysis System (ViCLAS), online description available: http://www.rcmp-grc.gc.ca/viclas/viclas_e.htm
[RSA] R.L. Rivest, A. Shamir, and L.M. Adleman, A method for obtaining digital signatures and public-key cryptosystems, Communications of the ACM (2) 21 (1978), 120-126.
[Sch] J. Schroeder, J. Xu, H. Chen, M. Chau, Automated criminal link analysis based on domain knowledge, Journal of the American Society for Information Science and Technology, volume 58 issue 6 pages 842-855 (2007).
[Sin] S. Singh, The Code Book, published 1999 by Fourth Estate. ISBN 1857028791. Online extracts are available: http://www.simonsingh.net/Crypto_Corner.html
[Smi] P. Smith and C. Panigl, RIPE Routing Working Group Recommendations on Route-flap Damping, ripe-378, available: http://www.ripe.net/ripe/docs/ripe-378.pdf
[Tar] Robert Tarjan, Depth-first search and linear graph algorithms. SIAM Journal on Computing. Vol. 1 (1972), No. 2, P. 146-160.
 Back to the LL.M. index.
Back to the LL.M. index.
 To my other legal topics index.
To my other legal topics index.
 Back to Clive's home page.
Back to Clive's home page.